О компанииСтатьиНапишите намНаш адресСправочник

Меню

Статьи

Расчет параметров взаимодействия через константу равновесия

Сводка данных о параметрах взаимодействия компонентов, растворенных в жидком железе, приведена в табл. 1. (более подробно значения параметров взаимодействия указаны в разделе "Параметры взаимодействия") В первой графе указаны элементы, активности которых изменяются под воздействием добавляемого компонента. Большая часть данных взята из справочника [1]. Для параметров взаимодействия кислорода с раскислителями приведены дополнительные данные, полученные главным образом В. Фишером с сотр. [2, с. 691...702].

Очевидно, что величина параметров взаимодействия между элементами-раскислителями и кислородом, растворенным в металле, должна зависеть от константы раскисления. Поскольку в результате раскисления образуются различные окислы, то, вероятно, будет правильно сравнивать константы раскисления, рассчитанные на 1 г-атом растворенного кислорода.

Если в результате раскисления образуется окисел RтОn, тогда для удельной (приходящейся на одни моль кислорода) константы раскисления, выраженной через проценты по массе, можно записать:

Kуд = [O]∙[R]m/n/(aRmOn)1/n (1)

Уравнение (1) справедливо лишь для разбавленных растворов в пределах применимости закона Генри. Более точной будет запись

Kуд = [O]∙[R]m/n∙fO∙fRm/n/(aRmOn)1/n (2)

Для обычных раскислителей коэффициентами активности fOO и fOR можно пренебречь в связи с малыми концентрациями кислорода. Однако для высокореактивных раскислителей, по-видимому, необходимо учитывать и концентрацию кислорода.

Однако уравнения (1) и (2) не могут быть приняты в качестве аргумента для параметров взаимодействия. По-видимому, рационально использовать молярную концентрацию раскислителя и относительное изменение активности кислорода при введении в расплав того или иного раскислителя. Учитывая это, константу раскисления, которую можно выбрать в качестве аргумента для функции εOR, запишем в следующем виде:

K* = aO∙aRm/n/(aRmOn∙γRm)1/n (3)

Активность кислорода выражаем через отношение молярной концентрации кислорода в данном расплаве к насыщенной молярной концентрации кислорода в равновесии с окислом данного металла при отсутствии в расплаве элемента-раскислителя, т. е.

aO = xO/xOнас∙fO (4)

Для разбавленных по кислороду растворов без существенной погрешности молярные концентрации можно заменить процентами по массе, тогда

aO = [O]/[O]нас∙fO (5)

В  разбавленном по компоненту R растворе мольная доля раскислителя будет равна

xR = [R]∙ArMe/{[R]∙ArMe + (100 - [R])∙ArR} ≈ [R]∙ArMe/(100∙ArR) (6)
где АMe и AR - атомные массы металла и раскислителя.

Подставляя (6) и (5) в уравнение (3), получим

K* = [O]∙[R]m/n/[O]нас∙{0,01∙ArMe/ArR}m/n∙fO∙fRm/n/(aRmOn)1/n (7)

Или учитывая выражение (2):

K* = Kуд/[O]нас∙{0,01∙ArMe/ArR}m/n (8)

С использованием значений параметров взаимодействия для расплавов на основе железа, приведенных в табл. 1, а также в работе [3] был проведен расчет приведенной удельной константы равновесия (K*) реакций окисления различных элементов кислородом (табл. 2). Иллюстрация расчетов представлена на рис. 1.

Логарифмическая зависимость параметров взаимодействия элементов-раскислителей с кислородом в расплавах железа при 1600 °С

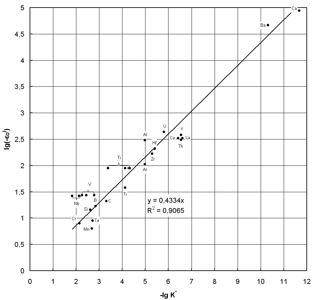
Рис. 1. Логарифмическая зависимость параметров взаимодействия элементов-раскислителей с кислородом в расплавах железа при 1600 °С

Обработка указанных данных позволила предложить следующее уравнение [4]:

lg(-εOR) = -0,43∙lgK* (9)

Учитывая уравнение (8), молярный параметр взаимодействия выразим через константы раскисления, % (по массе):

lg(-εOR) = -0,43∙{lgKуд - lg[O]нас - 2∙m/n + m/n∙lg(ArMe/ArR)} (10)

Переход от молярных к массовым параметрам взаимодействия следует производить по уравнению (11).

eij = 1/100∙1/ln10·{εij∙ArMe/Arj + (Arj - ArMe)/Arj} = 4,342·10-3·{εij∙ArMe/Arj + (Arj - ArMe)/Arj} (11)
где ArMe - атомная масса основного металла-растворителя, г/моль;
      ArR - атомная масса основного добавки (раскислителя); компонентом i может быть третий компонент, например, кислород, азот, водород и пр.

При больших параметрах взаимодействия или при близких значениях атомных масс раскисляемого металла и элемента-раскислителя уравнение (11) для растворов на основе железа упрощается до уравнения (12) и для любых других металлов можно записать

eiR = 1/100∙1/ln10·εij∙ArMe/ArR = εij∙ArMe/ArR∙1/230 (12)

Приняв упрощенную формулу (10) из уравнения (12) можно получить зависимость массового параметра взаимодействия от удельной константы равновесия:

lg(-еOR) = -0,43∙{lgKуд - lg[O]нас - 2∙m/n + m/n∙lg(ArMe/ArR)} + lg(ArMe/ArR) - 2,362 (13)

Учитывая, что уравнение (9) является полуэмпирической функцией, замена уравнения (11) на (12), по-видимому, не внесет существенных погрешностей.

Для растворов на основе железа с учетом температурной зависимости растворимости кислорода в железе под шлаком из окислов железа по известному уравнению

lg[О]нас = -6320/Т + 2,734 (14)

и уравнение (11) и (13) получим

lg(-еOR) = -0,43∙{lgKуд + 6320/Т - 2,734 - 2∙m/n + m/n∙lg(55,487) - m/n∙lgArR} + lg55,487 - lgArR - 2,362 (15)
lg(-еOR) = -0,43∙lgKуд - 2717,6/Т - 1,7934 - -0,11∙m/n - 0,43∙m/n∙lgArR - lg ArR (16)
lg(-еOR) = -0,43∙lgKуд + 2717,6/Т + 0,56 + 0,11∙m/n - (0,43∙m/n∙- 1)∙lgArR (17)

На рис. 1 нанесены экспериментальные данные по параметрам взаимодействия элементов-раскислителей с кислородом в расплавах никеля, кобальта и меди [2, с. 699...702; 5]. Экспериментальные точки для указанных металлов лежат вблизи прямой приблизительно с таким же разбросом, как и для расплавов на основе железа.

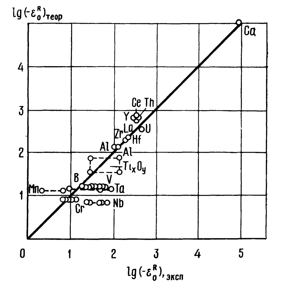
На рис. 2 приведено сравнение экспериментальных и расчетных величин εOR для железа, а на рис. 3 - для никеля, кобальта и меди.

Сравнение экспериментальных и расчетных данных Сравнение экспериментальных и расчетных параметров взаимодействия элементов-раскислителей с кислородом в никеле и кобальте
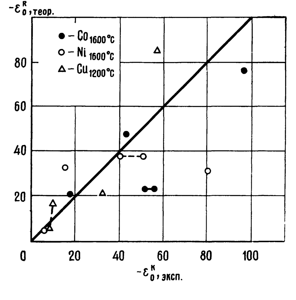
Рис. 2. Сравнение экспериментальных и расчетных данных по уравнению (10) параметров взаимодействия элементов-раскислителей с кислородом в железе при 1600 °С Рис. 3. Сравнение экспериментальных и расчетных по уравнению ((10) параметров взаимодействия элементов-раскислителей с кислородом в никеле и кобальте при 1600 °С и в меди при 1200 °С

Как видно из рис. 3 разброс экспериментальных точек значительный. Однако необходимо заметить, что и экспериментальные данные по параметрам взаимодействия по результатам разных исследований различаются в не меньшей степени. Так, например, по различным данным:

  • параметр eOTa 1873  равен  -0,12 [6]; -0,118 [7]; -0,065 [27]; -0,009 [2, с. 695...698]; 
  • параметр eOV 1873 равен -0,11 [8]; -0,13 [9]; -0,14 [10, 11]; -0,17 [12]; -0,227 [7]; -0,24 [13 с. 33]; 0,25...0,27 [14]; 0,29 [15];
  • параметр  eOTi 1873 равен  -0,137 [20, с. 245...256]; -0,158 [21]; -0,187 [22]; -0,36 [3]; -0,37 [23]; -0,45 [2 c. 695...698]; 0,65 [24]; 0,75 [3]; 1,12 [11].
Для алюминия в железе параметр взаимодействия eOAl, по данным ряда исследований, колеблется в пределах от -0,94 до -8 [1, 25, 12].

Отсюда следует, что данные, приведенные на рис. 2 и рис. 3, имеют разброс в пределах экспериментальных ошибок при определении параметров взаимодействия. Неточности при определении параметров взаимодействия экспериментальными методами обусловлены влиянием примесей, которые могут быть в исходном металле, а также и поступать в исследуемый расплав в результате химического взаимодействия расплава с материалом тигля либо с окислами раскисляемого металла и в результате изменения вида образующегося окисла с изменением концентрации раскислителя. Кроме того, параметры взаимодействия в бинарных системах являются функциями не только энергии взаимодействия и температуры, но и концентрации добавляемого элемента.

Вероятность ошибок при экспериментальном определении параметров взаимодействия увеличивается для высокореактивных металлов и высокореактивных окислов, а также для элементов, образующих серии окислов с близкими термодинамическими свойствами и обладающих широкими областями гомогенности.

Вопрос о температурной зависимости параметров взаимодействия в металлических расплавах рассматривался в ряде публикаций [16, с. 93; 26; 17, с. 174...176; 18; 19]. Так, например, Е. Нельсон [18] для растворов азота в железе предположил, что параметры взаимодействия являются линейными функциями обратной температуры. Д. Чипман и Д. Корриган [26] предположили линейную зависимость параметров взаимодействия от энтальпии компонентов в растворе.

Согласно уравнению (1), параметры взаимодействия пропорциональны константе раскисления в степени 0,43 или, как это видно из уравнения (17), логарифм абсолютного значения параметра взаимодействия является линейной функцией от обратной температуры, поскольку все прочие слагаемые, кроме lgКRmOn и lg[O]нac, от температуры не зависят.

Температурные функции параметров взаимодействия, таким образом, могут быть вычислены непосредственно из уравнений (10), (13), (17).

Если принять, что параметры взаимодействия eOR являются прямыми функциями энтальпии [26] или, точнее, изменения свободной энергии реакции раскисления металла, тогда зависимость параметров взаимодействия от удельной константы раскисления должна быть полулогарифмической функцией.

Такая зависимость приведена на рис. 4, из которого следует, что эти данные нельзя описать прямой линией, проходящей через начало координат.

Полулогарифмическая зависимость параметров взаимодействия элементов-раскислителей с кислородом от удельных констант раскисления

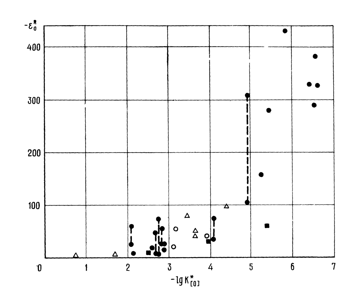
 Рис. 4. Полулогарифмическая зависимость параметров взаимодействия элементов-раскислителей с кислородом от удельных констант раскисления по экспериментальным данным для расплавов железа, никеля, кобальта и меди

На 4-м Японско-Советском симпозиуме по теоретической металлургии приведена следующая зависимость молярных параметров взаимодействия элементов-раскислителей с кислородом в расплавах элементов группы железа [4]:

lg(1 - 2∙εOR/z) = ψ∙(ΔGMeO° - ΔGRnOm° + 4,575∙lgγR(Me)°) (18)
где z - координационное число кислорода в жидком металле, равное 11;
     ΔGMeO° - стандартное изменение свободной энергии при образовании окисла МеО раскисляемого металла на 1 моль ксилорода;
     ΔG°RmOn - стандартное изменение свободной энергии при образовании окисла RmOn на 1 моль кислорода;
     lgγR(Me)° - коэффициент активности элемента-раскислителя в разбавленном растворе.

При положительных значениях свободной энергии (более 20 ккал) получена линейная зависимость. Это подтверждает уравнение (9). В комментарии к докладу по рассматриваемому вопросу [4] С. Мизогучи и Я. Накамура аналитически вывели следующее уравнение:

lg(-εOR) = -m/n∙{lgK2 - lgNO + lglg(NOR/NO)} (19)
где K2 = aO∙aRm/n
      NO - растворимость кислорода в чистом железе;
      NOR- содержание кислорода в железе при наличии раскислителя в точке равновесия жидкого железа с чистыми окислами FeO и элемента-раскислителя.

Все это свидетельствует о правильности выбора формы уравнения (9) для элементов-раскислителей. Поэтому в дальнейшем при анализе раскисления металлов для вычисления параметров взаимодействия были использованы формулы, вытекающие из уравнения (9).

Список использованной литературы

  1. Эллиот Д. Ф., Глейзер М., Рамакришна В. Термохимия сталеплавильных процессов. М.: Металлургия, 1969. 252 с.
  2. Arch. Eisenhuttenw. 1971. Bd. 42. № 10. S. 691...702.
  3. Buzek Zd., Macoszek M., Szlaver J. Hutnicke Listy. 1972. T. XXVIII. № 8. S. 547...557.
  4. Kulikov I. S. The fourth Japan-USSR joint symposium on physical chemistry of metallurgical processes, 1973. Tokyo. The Iron and Steel Inst. Japan, (21). P. 1...14, fig. 4.
  5. Fischer W. A., Janke D. Z. Metallkunde. 1971. Bd 62. № 10. S.747...751.
  6. Scala J., Mandi М. \ Vyskumna Sprava VUHZ. 1963, Praha.
  7. Naritа К., Коjama S. \ Trans. Iron and Steel Inst. Japan. 1969. V. 9. № 1. P. 53...58
  8. Schenck Н., Steinmetz E. \ Arch. Eisenhiittenw. 1967. Bd 38. S. 851...853.
  9. Сюй-Цзя-лун, Кашин В. И., Поляков А. Ю., Самар и н А. М. \ Изв. АН СССР. Металлургия и горное дело. 1964. № 6. C. 75...80 с ил.
  10. SanbongiK., Omori Y. \ Tetsu-to-Hagane. 1968. V. 48. № 11. P. 1292...1295.
  11. Fruehan R. J. \ Metal. Trans. 1970. V. 1. № 12. P. 3403...3410
  12. Самарин А. М. Физико-химические основы раскисления стали. М., Изд-во АН СССР. 1956. 161 с.
  13. Поляков А. Ю. Основы металлургии ванадия. М., Изд-во АН СССР. 1959. 160 с.
  14. Dustur N. N., Chipman J. \ J. Metals. 1951. P. 111...115.
  15. Pargeter J. К.  \ Can. Met. Quart. 1967. V. 6. P. 21...36.
  16. Кунин Л. Л., Головин А. М., Суровой Ю. Н. и др. Проблемы дегазации металлов. М.: Наука. 1972. 327 с.
  17. Суровой Ю. Н. Теория металлургических процессов. М. Металлургия, 1969 (ЦНИИЧМ. Сб. № 70). 184 с. с ил.
  18. Nelson Е. С. \ Trans. AIME. 1963. V. 227. P. 189...191.
  19. Chipman J. \ Trans. Iron and Steel Inst. Japan. 1966. V. 6. P. 207...213.
  20. Ляудис Б. К., Самарин А. М. Физико-химические основы производства стали. М., Изд-во АН СССР. 1957. 800 с. с ил.
  21. Suzuki К., Omori Y., Sanbongi К. Bull. Res. Inst. Min. Dress. Met. Rep. Tohoku Univ. 1967. V. 23. P. 137...146.
  22. Chipman J. \ Trans. Met. Soc. AIME. 1960. V. 218. P. 767...768.
  23. Koyima Y., Inouye М., Ohi J. \ Arch. Eisenhuttenw. 1969. Bd 40. S. 667...671.
  24. Явойский В. И. Физика металлов. 1971. Т. 42. С. 50...58.
  25. Rohde L. E., Choudhury A., Walsher М. \ Arch. Eisenhuttenw. 1971. Bd 42. № З. S. 165...173.
  26. Chipman J., Corrigan D. A. \ Trans. Met. Soc. AIME. 1965. V. 233. P. 1249...1256.
  27. Аверин В.В. Растворимость кислорода, азота и активность элементов-раскислителей в расплавах на основе железа, кобальта, никеля и хрома. Автореф. дисс. докт. техн. наук. М.: Имет  АН СССР. 1968. 32 с.

Замечания, комментарии и вопросы к данной статье Вы можете отправить здесь. Мы Вам обязательно ответим.

Табл. 1. Молярные (числитель) и массовые (знаменатель) параметры взаимодействия в жидком железе при 1600 °С

  Добавляемый элемент j
i Al В V О Co Si Mn Nb S Ta Ti C Cr
N 0,3   -21 3,3 2,7 5,4 -4,5 -25,7 1,7 -25 -120 6,4 -9,6
-0,002   -0,1 0,0608 0,0109 0,0423 -0,02 -0,065 0,0096 -0,031      
Al 5,3     0,8203   70     6,5     5,3  
0,043     -1,581   0,6002     0,0459        
В       -17                  
      -0,247                  
V       -27,1               -80  
      -0,4               -1,631  
Н   2,2     0,44 3,2 -0,32 -0,88 1,1 15 -16 3,2 -0,47
  0,0313     0,0016 0,0233 -0,001 -6E-04 0,0051 0,0231 -0,082 0,0488 -0,003
W       6,4         1     2,3  
      0,1078         0,0043     0,0306  
Hf       -208,2         -35,3        
      -3,145         -0,27        
Аu       -3                  
      -0,035                  
Y       -171         -101        
      -2,581         -0,767        
О -105 -17 -27,1 -13 1,7 -14,5 -6,3 -26,4 -12 -9 -89 -21 -8
-0,949 -0,399 -0,129 -0,208 0,0068 -0,13 -0,028 -0,067 -0,094 -0,009   -0,44 -0,038
Со       1,7         0,67     2,9  
      0,0366         0,0018     0,0427  
Si 7     14,5   37     8     12  
0,0583     0,2306   0,3152     0,0573     0,2265  
La       -330         -123        
      -4,992         -0,934        
Mn       -6,3         -5,3        
      -0,085         -0,043        
Сu       -2,5         -3,9     4,2  
      -0,027         -0,033     0,069  
Mo       2,2         0,07     -3,5  
      0,0442         -0,003     -0,087  
Ni       1,4   1,2     -1,3     2,9  
      0,032   0,0061     -0,013     0,0427  
Nb       -26,4       3,2 -6,5     -23  
      -0,389       0,0101 -0,052     -0,48  
Sn                       14,4  
                      0,2749  
Pt       3,6                  
      0,0654                  
Se             -5,2            
            -0,023            
S 6,5/3,2     -12 0,67 8   -6,5 -3,7 -17 -16 9 -3,6
0,0538     -0,171 0,0025 0,0648   -0,015 -0,031 -0,02 -0,082 0,1659 -0,017
Sc       -240         41        
      -3,627         0,3069        
Та       -9         -16,8        
      -0,126         -0,13        
Ti       -89         -16   9    
      -1,338         -0,124   0,0449    
C 5,3   -8 -21 2,9 12   -23 9     11 -5,1
0,043   -0,039 -0,308 0,0117 0,0993   -0,058 0,0649     0,2063 -0,024
P       8,9   11     5,7        
      0,1457   0,0907     0,0399        
Cr       8         -3,6     -5,1  
      0,1321         -0,03     -0,119  
Ca       -88000                  
      -1334                  
U       -433         -69        
      -6,553         -0,525        
Zr       -167         -26        
      -2,521         -0,2        
Ce                 -135        
                -1,024        

Табл. 2. Результаты расчета приведенной константы равновесия реакций окисления различных элементов

  Al2O3 AlO B2O3 VO V2O3 VO2 SiO2 MnO NbO
Ar(R) 26,98 26,98 10,81 50,9415 50,9415 50,9415 28,09 54,94 92,9064
εOj -105 -305 -17 -27,1 -27,1 -27,1 -14,5 -6,3 -26,4
lg(-εOj) 2,021 2,484 1,230 1,433 1,433 1,433 1,161 0,799 1,422
-lgK* 4,97 4,97 2,84 2,43 2,79 2,25 2,61 2,69 2,16

табл. 2. Продолжение

  Nb2O3 Nb2O5 TiO Ti2O3 Ce2O3 UO2 ZrO2 HfO2 ThO2
Ar(R) 92,9064 92,9064 47,88 47,88 140,12 238,00 91,20 178,50 232,00
εOj -26,4 -26,4 -89 -89 -330 -433 -166,6 -208,2 -308,2
lg(-εOj) 1,422 1,422 1,949 1,949 2,519 2,636 2,222 2,318 2,489
-lgK* 2,13 1,83 4,28 4,32 6,60 5,81 5,29 5,40 6,55

табл. 2. Продолжение

  Ti3O5 TiO2 TiO3 CO2 Cr2O3 CaO BaO Y2O3 La2O3
Ar(R) 47,88 47,88 47,88 12,01 52,00 40,08 137,33 88,91 138,91
εOj -89 -38 -89 -21 -8 -88000 -46537,5 -380 -330
lg(-εOj) 1,949 1,580 1,949 1,322 0,903 4,944 4,668 2,580 2,519
-lgK* 4,12 4,12 3,38 3,31 2,14 11,68 10,32 6,55 6,42

 

Наши партнёры

Спец-предложение

Предлагаем услуги по оптимизации геометрии разливочной оснастки с целью обеспечения повышения коэффициента использования металла и снижения осевой пористости слитков

подробнее
О компанииСтатьиНапишите намНаш адресСправочник
© 2009
Создание сайтов в студии Мегагрупп

При копировании материалов сайта размещение активной ссылки на steelcast.ru обязательно | статьи партнеров

Rambler's Top100
Расчет параметров взаимодействия через константу равновесия