Параметры взаимодействия
Физико-химические расчеты конкретных металлических систем требуют знания активностей элементов в многокомпонентных системах. Наиболее простую и доступную возможность расчета активностей представляет использование параметров взаимодействия, учитывающих влияние каждого из имеющихся компонентов на определяемый коэффициент активности. Основу метода составляет разложение соответствующей парциальной избыточной термодинамической функции смешения (энергии Гиббса ΔGie, энтальпии ΔHi, энтропии ΔSie) в степенной ряд Тейлора (Маклорена) по концентрациям компонентов и обратной температуре около точки, отвечающей чистому растворителю. Если за стандартное состояние принять чистый компонент i, то для избыточной свободной энергии, точнее для lnγi = ΔGie/(R·T) при постоянных температуре и давлении получим:
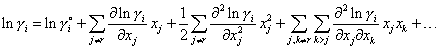
|
(1) |
Здесь и далее суммирование производится от единицы до n, а частные производные соответствуют точке чистого растворителя (xr = 1). Входящие в уравнение частные производные называют параметрами взаимодействия и обозначают соответственно εij, ρij и ρij,k. С учетом этих обозначений выражение (1) принимает вид:
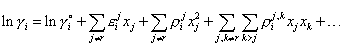
|
(2) |
Аналогичные выражения можно записать для ΔHi и ΔSie. Наиболее часто используют формулы Вагнера в виде ряда, в котором отброшены слагаемые выше первого порядка.
В точке xr=1 параметры имеют строгий термодинамический смысл, а следовательно, единственное значение, к которому должны стремиться накапливаемые экспериментальные величины. Это и является основой для табулирования таких данных. Разложение Вагнера (как и любой ряд) можно использовать и в концентрационном интервале (фактически оно так и используется), однако параметры разложения при этом утрачивают свойства термодинамически обоснованных констант, становятся обычными коэффициентами аппроксимирующего полинома, характеризуют частный массив данных и должны приводиться с указанием интервала составов, в котором производилось определение численных величин параметров. Однако в литературе часто не различают параметры Вагнера, как фундаментальные константы вещества и частные аппроксимирующие коэффициенты. Поэтому не случайно, что приводимые различными авторами значения "параметров Вагнера" могут не совпадать по знаку и порядку величины, не соблюдается требуемое теорией тождество εij = εji. Табулирование таких данных утрачивает упомянутую выше строгую основу, на которой, собственно, базируется метод Вагнера.
В случае выбора стандартного состояния по Льюису (однопроцентный идеальный разбавленный раствор компонента i в растворителе) разложение в ряд Тейлора приводит к следующему выражению:
lgfi = eii·[i] + Σeij·[j]
|
(3) |
Переход от молярных к массовым параметрам взаимодействия первого порядка и обратно следует производить по приведенным в работе [1] уравнениям (4)...(7).
где ArMe - атомная масса основного металла-растворителя, г/моль;
ArR - атомная масса основного добавки (раскислителя); компонентом i может быть третий компонент, например, кислород, азот, водород и пр.
В некоторых справочниках приведены значения параметров взаимодействия для температуры, отличной от 873 К. Для приведения значений к 1873 К может быть использовано уравнение (8), вытекающее из основных положений квазихимической теории, когда, в частности, энергия смешения принимается равной соответствующим предельным теплотам растворения.
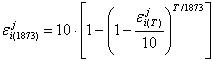
|
(8) |
Из этой же теории вытекает соотношение, позволяющее пересчитать на температуру 1873 К коэффициент активности в бесконечно разбавленном растворе.
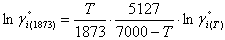
|
(9) |
Значение молярных и массовых параметров взаимодействия первого порядка приведены в таблице 1, значения параметров взаимодействия второго порядка - в таблице 2. Если есть желающие, кто может предоставить данные по параметрам взаимодействия второго порядка - будем рады сотрудничеству. Список использованных источников
- Sigworth G. K., Elliot J. F. The thermodynamics of liquid dilute iron alloys \\ Metal science Journal. 1974. V. 8. № 9. P. 298...310.
|